PGNN

Jiaxuan You / Position-aware Graph Neural Networks / ICML(2019)

1. Problem Definition

Position-aware Embeddings?

A node embeddings , is position-aware if there exists a function such that is the shortest path distance in

본 논문에서는 Graph Neural Networks(이하 'GNN')에서 Position-aware의 성질을 반영할 수 있는 방안에 대해서 다루고 있다. Position-aware Embedding이란 위 정의처럼 Embedding Space에서도 두 Node간 Shortest Path Distance가 유지되도록 임베딩하는 것을 의미한다.

Structure-aware Embeddings?

A node embeddings is structure-aware if it is a function of up to q-hop network neighbourhood of node

다른 개념으로 Structure-aware가 있다. 기존의 GNN 모델들 중 GCN, GAT처럼 Target Node의 q-hop의 neighbor를 이용해서 message-passing하는 경우 그래프의 structure를 반영하여 임베딩할 수 있기 때문에 이를 Structure-aware Embedding이라고 한다.

Key Insights

논문에서는 2가지의 Key Insights를 제시하고 있다.

1. 그래프의 Position 정보를 어떻게 반영할 것인가? Anchors-sets를 이용해서 각각의 set에서 나오는 메시지를 Aggregation하여 Position 정보를 반영한다. 2. Position의 기준이 되는 Anchor-sets들은 어떻게 구성할 것인가? Bourgain Theorem를 이용하여 이론적 근거를 바탕으로 Position-aware한 임베딩을 할 수 있는 Anchor Set를 구성한다.

Goal

최종적인 목표는 그래프 내 노드의 global position을 반영하면서도, 노드 주변의 local structure를 반영할 수 있는 Position-aware Graph Neural Networks(이하 'PGNN')를 만드는 것이다.

2. Motivation

기존 GNN은 노드들이 symmetric이나 isomorphic한 position에 있는 경우 이 두 노드들을 구분할 수 없다는 문제점이 있다. 이 문제를 다루기 위해서 heuristic한 방법을 쓰기도 하는데, 각 노드들마다 unique identifier를 할당시켜주거나, 와 같이 position의 기준이 되는 identifier를 정해준 뒤, transductive하게 그래프를 사전학습시키는 방법이 있다. 허나 이러한 방법들은 모두 scalable하지 못하고, 처음보는 그래프에 대해서는 기존에 정해두었던 identifier를 활용할 수가 없기 때문에 general하지 못한 단점이 있다. 따라서 PGNN은 기존의 Structure-aware GNN의 장점을 그대로 가져가면서 positional 정보도 함께 임베딩하는 것을 목표로 한다.

3. Method

Architecture

PGNN의 전체 Architecture는 위와 같다. 먼저 k개의 anchor-set를 만들고, 각각에 anchor-set에 노드들을 할당한다. k는 어떻게 정해지는 지, 그리고 노드들의 할당은 어떻게하는 지는 후술하도록 하겠다. 그리고 각 노드에 대해서 임베딩을 하게 되는데 을 임베딩한다고 하면, 과 나머지 노드들에 대해서 짝을 짓고, 각 anchor-set에 속하는 노드들의 정보만 모아서 anchor-set 개수만큼의 메시지를 만든다. 그 후 총 2개의 output이 나오게 된다.

하나는 anchor-set 위치에 대해서 invariant한 임베딩()이 나오게되고, 나머지 하나는 최종적으로 우리가 task를 수행하는 데 필요한 임베딩()이 나온다. 이렇게 2개의 output을 둔 이유는, 모델의 expressive power를 높이려면 layer를 여러 개 쌓는 것이 필요한데, 최종 output인 는 다음 layer에 전달을 줄 수가 없기 때문이다. 그 이유는 anchor-sets는 한 사이클이 돌 때 마다 다시 뽑히게 되는데, 가 담고 있는 정보들은 이전 layer에서 뽑힌 anchor-set에 대해서 relative한 정보를 담고 있기 때문에, 다음 layer에서는 쓸 수 없는 정보이다. 그렇기 때문에 multi-layer를 쌓기 위해서, 각 set에서 나온 메시지들을 mean aggregation을 통해 set들에 대해 invariant한 output을 만들고, 이를 다음 layer로 전달하게 된다. 결국 임베딩은 multi-layer 학습을 할 때만 쓰이고, 마지막 output인 는 마지막 layer에서 뽑힌 anchor-set를 기준으로 positional한 정보를 담고있는 임베딩이 된다.

의 dimension은 anchor-set의 개수만큼 나오고, 각각의 dimension은 그 anchor-set와의 distance 정보를 담고 있다.

Anchor-set Selection

이제 중요한 것은 몇 개의 anchor-set를 만들어야하고, 노드들은 어떻게 할당할 것인가인데, 본 논문에서는 Bourgain Theorem를 근거로 둔다.

Theorem 1 : Bourgain Theorem Bourgain Theorem guarantees that only anchor-sets are needed to preserve the distances in the original graph with low distortion () : # of nodes

간단하게 요약하자면, 그래프 내 노드의 global position을 임베딩하기 위해서는 개의 anchor-set만 만들면 충분하다는 것이다. 더 자세하게는 distortion이 을 넘지 않게끔 positional embedding을 할 수 있다고 한다.

Definition : Low distortion embedding Given two metric spaces and and a function , is said to have distortion if : distance function

distortion이란 한 metric space에서 다른 metric space로 임베딩하는 function 가 있다고 했을 때, 과 같은 관계가 성립하면 만큼의 distortion이 있다고 말한다. 즉, 의 값이 1에 가까울수록 distance가 최대한 보존이 되는 임베딩이 된다고 보면 된다.

Theorem 2 : Constructive Proof of Bourgain Theorem For metric space , given random sets where is constant, is chosen by including each point in independently with probability . An embedding method for is defined as :

where . Then is an embedding method that satisfies Theorem 1.

위 예시는 Theorem 1에서 정의한 Bourgain Theorem을 만족시키는 예를 들고 있다. 위 방법대로 이해하기 쉽도록 구체적인 예시를 들어보겠다.

Example of Anchor-set Selection

인 경우, 이다. 즉, 는 각각 (1,2), (1,2,3,4)의 경우의 수로 존재할 수 있는데 따라서 총 개의 anchor-set를 생성하게 된다. 각각의 anchor-set에 노드를 할당하는 경우, 그래프의 모든 노드에 대해서 해당 anchor-set 속할 확률은 이므로, 인 set는 50%의 확률로 할당하고, ㅇ 인 경우, 이다. 즉, 는 각각 (1,2), (1,2,3,4)의 경우의 수로 존재할 수 있는데 따라서 총 개의 anchor-set를 생성하게 된다. 각각의 anchor-set에 노드를 할당하는 경우, 그래프의 모든 노드에 대해서 해당 anchor-set 속할 확률은 이므로, 인 set는 50%의 확률로 할당하고, 인 set는 25% 확률로 할당을 하게 된다.

이런식으로 할당을 하게 되면, anchor-set의 사이즈가 exponential하게 다양하게 만들어진다. 즉, 노드가 적게 포함된 set와, 많이 포함되는 set가 다양하게 만들어지게 된다. 노드가 적게 포함된 set는 position을 특정하기에 좋은 정보를 주지만, 애초에 어떤 노드를 포함시킬 확률이 낮기 때문에, 만약에 그 노드를 anchor-set에 포함시키지 못하게 된다면, 그 노드의 정보 자체를 반영하지 못한다는 단점이 있다. 이에 반해, 노드가 많은 set는 각 노드들이 포함될 확률이 높기 때문에 위와 같이 노드를 놓쳐서 정보를 반영하지 못하는 문제는 없지만, 포함된 노드가 너무 많으면 position을 특정하기 어렵다는 문제가 있다. 그렇기 때문에 여러가지 사이즈의 anchor-set를 사용함으로써 위 2가지 케이스의 trade-off를 균형있게 맞출 수 있다고 보면 된다.

PGNN

위와 같이 Bourgain Theorem을 만족시키는 함수를 generalization한 것이 PGNN이며, Bourgain Theorem 1의 식에 포함된 distance metric d를 message computation하는 function 와 aggregation function 을 정의했다.

Message Passing Function, F

Position 정보를 담는 빨간 박스 부분과, 기존의 일반적인 message passing을 할 때 쓰이는 feature를 전달하는 부분이 있다. 여기서 두 노드들의 feature를 concat하여 전달하게 된다.

function s는 q-hop내의 노드들에 대해서 shortest path distance를 구하는 함수이다.

Aggregation function, AGG

Aggregation function은 anchor-set 위치에 대해서 invariant한 성질을 줄 수 있는 MEAN, MIN, MAX, SUM 등을 사용할 수 있는데, 여기서는 MEAN을 사용하였다.

Summary

다시 정리하면, 2 layer라고 가정했을 때 최종 output을 생성하는 과정은 다음과 같다.

Anchor-set를 생성
각 노드들에 대해서 다른 노드들과 페어를 만든 후
function F로 message computation
같은 Anchor set에서 나온 message들을 aggregation하는 데, 다음 layer에 임베딩을 전달해주기 위해서 MEAN aggregation
다음 layer에서 다시 anchor-set를 생성
각 노드들에 대해서 다시 임베딩한 후, 각 anchor-set에서 나온 messsage들을 w라는 weight를 이용하여 최종 output 생성

4. Experiment

본 논문에서는 link-prediction과 node classification task 2가지의 실험을 진행하였다.

Experiment setup

Dataset

Link Prediction Dataset

Grid : 2D (20x20)의 grid graph 데이터이며, 노드의 개수는 400개, 노드 feature는 존재하지 않는다.
Communities : 1%의 edges들이 랜덤으로 rewired된 Connected caveman graph이다. 각각 20개의 노드로 이루어진 20개의 communities로 이루어져있다.
PPI 24개의 Protein-Protein interaction networks이다. 각 그래프는 3000개의 노드로 이루어져 있고, 평균적으로 28.8개의 degree를 가지고 있다. 각 노드들은 50dim의 feature를 가지고 있다.

Node Prediction Dataset

Communities : Link prediction dataset에서 설명한 바와 같다.
Emails : 7개의 real-world email communication graphs from SNAP. 노드 feature는 없으며, 각 그래프는 6개의 communites가 있고, 각 노드들은 어떤 community에 속하는 지 라벨링되어 있는 데이터셋이다.
Protein 1113개의 protein graphs이다. 각 노드들은 protein에서 어떤 functional role을 하고 있는 지에 대해 라벨링 되어있고, 각 노드 feature는 29dim이다.

baseline

baseline 모델들은 기존의 GNN에서 대표적인 모델들과 비교를 하였다. 본 논문 이전에 position을 explicit하게 반영하는 GNN 모델들이 없기 때문이다.

GCN : GCN은 Fourier transform을 그래프에 접목시켜서 graph convolution을 가능하게 한 모델이다. GAT에 비해서 graph의 global한 feature를 반영하기에 적합하다.
GAT : GAT는 GCN과는 다르게 주변 노드들을 aggregation하여 임베딩하는 데, 이렇게 때문에 GCN에 비해서 더 flexible하며, adaptive한 성질을 가지고 있다.
GraphSAGE : 이웃 노드들 중에서 고정된 개수의 노드들을 샘플링하여 feature를 aggregation하는 방법으로 효과적으로 노드 임베딩하는 모델이다.
GIN : 동형(isomorphic)이 아닌 그래프를 구분할 수 있는 모델이다.

Evaluation Metric

Link Prediction Dataset

두 노드가 link로 연결되어 있는 지에 대해 prediction하고 이에 대한 ROC AUC를 측정하였다.

Pairwise node classification

두 노드가 같은 community에 속해 있는 지, 아닌 지에 대해서 prediction하는 task이다. 일반적으로는 node의 label을 맞추는 task를 node classification이라고 하나, 본 논문에서는 비슷한 neighbor structure를 가지고 있는 두 노드들을 구분할 수 있는 지에 대한 정확도를 측정하기 위하여 이와 같이 실험하였다고 한다. 이 또한 ROC AUC를 측정하였다.

Result

Link Prediction

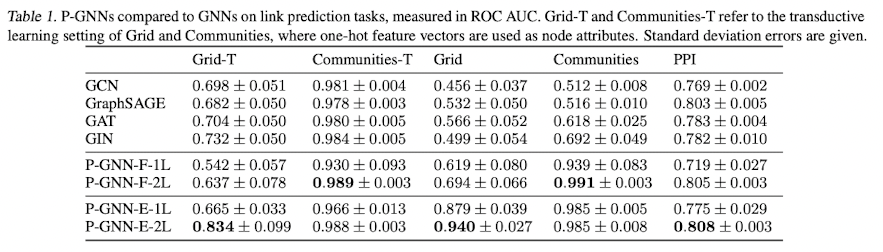
위 실험에서, 노드 feature가 없는 데이터셋에 대해서는 feature가 있는 PPI 데이터셋보다 성능이 굉장히 높은 것을 확인할 수 있다. 하지만 PPI의 경우에는 성능이 기존 모델들에 비해서 겨우 좋은 성능을 보이고 있다. 이에 대해서 feature가 어느 정도 높은 dimension을 가지고 있는 경우에는 노드 feature 자체가 position의 정보를 어느 정도 대체할 수 있지 않은 지 생각해볼 수 있다. 본 논문에서 노드 feature가 position의 정보를 얼만큼 담고 있는지에 대한 future work도 함께 던지고 있다.

Node Classification

위 실험에서도 노드 feature가 없는 데이터셋에 대해서는 성능이 좋은 모습을 보이고 있다. Protein 데이터셋에서도 29 dimension의 노드 feature가 있음에도, position을 함께 반영하는 것이 더 좋은 성능을 보이고 있다. 하지만 본 실험만 봐서는 노드 feature가 있는 데이터셋들에 대해서 position이 과연 얼마나 더 좋은 영향을 미치고 있는가를 파악하기 어려운 점이 있다. 이에 대해서 노드 feature가 있는 데이터셋을 dimension에 따라 더 많이 실험을 해줬으면 어땠을까라는 생각이 든다.

5. Conclusion

요약하자면, PGNN은 기존의 Structure-aware한 GNN의 성질을 유지하면서, Position-aware한 성질까지 결합한 GNN 모델이다. Bourgain Theorem으로 그 이론적 근거에 대해서 탄탄히 설명을 하였고, 이를 기반으로 Anchor-set를 생성하여 Complexity를 줄이면서 position을 효과적으로 임베딩하는 방법에 대해서 제시하였다.