Latent ODEs

Y Rubanova et al./ Latent ODEs for Irregularly-Sampled Time Series / NeurIPS-2019

Latent ODEs for Irregularly-Sampled Time Series

1. Problem Definition

시계열 데이터를 다루는 Deep learning에 미분방정식 (Ordinary Differential Equation) 을 접목시키자!

본 논문은 continuous-time dynamics를 가지는 RNN(Recurrent Neural Networks)의 hidden dynamics를 ODEs(Ordinary Differential Equations)로 정의해 새로운 모델 ODE-RNN을 만들어냅니다.

또한 NeurIPS에 2018년에 publish 된 'Neural ordinary differential equations' 라는 논문에서 제시한 Latent ODE model의 recognition network을 ODE-RNN으로 대체합니다. 이를 통해 관측값 사이의 임의의 time gap을 다룰 수 있습니다.

2. Motivation

기존 Continual learning 방법들은 Image같은 grid domain에만 집중하고, Graph같은 non-grid domain은 간과했다!

RNN은 regularly-sampled time series data에 대해 좋은 성능을 보이나, data의 time-gap이 불규칙적인 경우 좋은 성능을 내지 못합니다.

이에 지금까지 사용하던 몇 가지 해결책이 있었는데,

• timeline을 equally-sized intervals로 나누거나,

• observation들을 평균을 사용해 impute/agrregate 하는 등의 간단한 trick을 사용했습니다.

하지만 이러한 방식은 measurement의 timing 같은 정보량을 줄이거나 왜곡하는 문제가 있었습니다.

이에 저자들은 모든 time point에 정의된 latent space를 가지는 continuous-time model을 정의하고자 합니다.

RNN과 ODE-RNN의 hidden state trajectory

예를 들어, 위 사진은 RNN과 저자들이 제시한 ODE-RNN의 차이를 보여줍니다. 각 line은 hidden state의 trajectory를 나타내고 수직 점선은 observation time을 나타내는데, RNN은 observation이 나타날 때만 hidden state에 변화가 있어 각 observation 사이를 예측하긴 어렵습니다.

반면에 ODE-RNN은 각 observation 사이에도 trajectory를 fitting하며 observation이 들어올 때 마다 값을 수정해주는 것을 확인할 수 있습니다. 이런 식으로 ODE-RNN은 observation이 불규칙적으로 있어도 좋은 예측 성능을 보일 수 있습니다.

3. Method

Preliminaries: What are RNN, Nerual ODE, Variational Autoencoder?

논문에서 제안한 방법론을 이해하기 위해서는 RNN, Neural Ordinary Differential Equations, 그리고 Variational Autoencoder의 개념을 알고 있어야 합니다.

본 포스팅에서는 간단하게 소개를 하겠으며, 세 가지 방법론에 대해 자세히 알고 싶으시면 각각 여기, 여기, 그리고 여기를 참고하시기 바랍니다.

1. RNN

RNN은 hiddent layer에서 나온 결과값을 output layer로도 보내면서, 다시 다음 hidden layer의 input으로도 보내는 특징을 가지고 있습니다.

아래 그림을 보시겠습니다.

RNN의 구조

$x_{t}$ 는 input layer의 input vector, $y_{t}$ 는 output layer의 output vector입니다. 실제로는 bias $b$ 도 존재할 수 있지만, 편의를 위해 생략합니다.

RNN에서 hidden layer에서 activation function을 통해 결과를 내보내는 역할을 하는 node를 셀(cell)이라고 표현합니다. 이 셀은 이전 값을 기억하려는 일종의 메모리 역할을 수행하므로 이를 메모리 셀 또는 RNN 셀이라고 합니다.

이를 식으로 나타내면 다음과 같습니다.

• Hidden layer: $h_{t}=tanh(W_{x}x_{t}+W_{h}h_{t-1}+b)$
• Output layer: $y_{t}=f(W_{y}h_{t}+b)$

Hidden layer의 메모리 셀은 각각의 시점(time step)에서 바로 이전 시점에서의 메모리 셀에서 나온 값을 자신의 입력으로 사용하는 재귀적(recurrent) 활동을 하고 있습니다. 그러나 그림에서 보이듯이, RNN은 각 time step에서만 정보를 처리하므로 time step이 불규칙적이거나, 각 time step 사이의 값에 대해서는 예측 성능이 좋지 않습니다.

또한, RNN이 가진 문제를 해결한 RNN-Decay, GRU 등 다양한 모델이 있으나 본 포스팅에서 설명은 생략하겠습니다.

저자들은 이런 discrete한 hidden layer를 ODE를 사용해서 continuous하게 바꾸려는 겁니다.

2. Neural Ordinary Differential Equations

Neural ODE는 continuous-time model의 일종으로, 지금까지 discrete하게 정의되었던 hidden state $h_{t}$ 를 ODE initial-value problem의 solution으로 정의합니다. 이를 식으로 나타내면 다음과 같습니다.

$dh_{t}/dt=f_{\theta}(h(t),t) where h(t_{0})=h_{0}$

여기서, $f_{\theta}$ 는 hidden state의 dynamics를 의미하는 neural network입니다. Hidden state $h(t_{0})$ 는 모든 시간에 대해 정의되어있으므로, 어떠한 desired time에 대해서도 아래의 식을 통해 evaluate 될 수 있습니다.

$h_{0},...,h_{N}=ODESolve(f_{\theta},h_{0},(t_{0},...,t_{N}))$

위 식으로 우리는 hidden layer를 continuous 하게 정의할 수 있으며 이 방식은 다음과 같은 장점들이 있습니다.

• Discrete한 hidden layer를 사용할 때는 각 layer마다 parameter가 있었으나, 이 방식은 하나의 parameter($\theta$)로 연산 가능하여 computational cost가 적습니다.
• Hidden layer가 연속적인 하나의 layer로 생각될 수 있으므로, interpolation이나 extrapolation 등의 예측에 뛰어납니다.

3. Variational Autoencoder

Variational Autoencoder(VAE)는 측정 불가한 분포를 갖는 어떤 잠재변수로부터 효과적인 근사 추론을 하는 것이 목적인 모델입니다. 유명한 deep generative model인 GAN과 같은 생성 모델의 일종이며, 구조가 Auto-encoder와 비슷해 이름이 이렇게 붙여졌습니다.

VAE의 구조

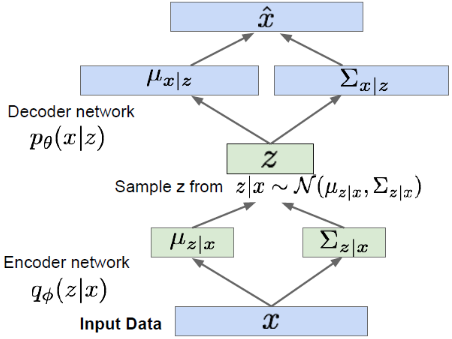
위 그림을 간단하게 설명하자면, 어떤 input data $x$ 가 있을 때, Encoder network가 잠재변수 $z$ 의 분포(평균과 분산)을 근사합니다. 만들어진 분포에서 $z$ 를 sampling 하고 Decoder network는 $\hat{x}$ 을 만들어냅니다.

본 논문에서 저자들은 이 VAE의 구조 중 Encoder network에 ODE-RNN을 쓰고 Decoder network에 RNN을 사용한 Latent ODE를 소개합니다.

ODE-RNN

앞서 설명드린 바와 같이, ODE-RNN은 RNN의 discrete한 hidden layer에 ODE를 통해 continuous한 정보를 담게 하는 모델입니다.

그 방법은 굉장히 단순한데, Neural ODE를 사용한 hidden state를 정의해서, RNN cell에 정보를 흘려보내주는 겁니다.

ODE-RNN이 작동하는 원리는 아래와 같습니다.

ODE-RNN의 알고리즘

위 알고리즘을 설명해보면, 저자들은 각 observation 사이의 state을 다음과 같이 하나의 ODE의 solution으로 정의했습니다.

$h'_{i}=ODESolve(f_{\theta},h_{i-1},(t_{i-1},t_{i}))$

그리고 각 observation의 hidden state는 기본 RNNcell로 해주면, $h_{i}=RNNCELL(h'_{i},x_{i})$ 과 같이 되게 됩니다.

이것이 ODE를 RNN에 접목시킨 아이디어의 전부입니다.

그러면 지금까지 RNN과 ODE-RNN을 알아보았는데요, 그들의 hidden state가 어떻게 정의되는지를 보면 다음과 같습니다. (RNN-Decay와 GRU-D 또한 RNN의 일종이라고 생각하시면 됩니다)

Definition of hidden state

앞서 설명해드린 바와 같이, RNN 기반 모델들은 각 observation이 있을 때만 discrete한 hidden state가 정의되는 반면에 ODE-RNN 모델은 각 observation 사이 시간도 고려합니다.

위의 모델들은 저자들이 모델의 성능을 평가하기 위한 baseline으로 사용합니다.

RNN의 Discrete한 layer 사이에 continuous한 하나의 ODE로 모든 time step의 정보를 저장한다!

Latent ODEs

앞서 소개한 RNN이나 ODE-RNN은 autoregressive model이라고 합니다. Autoregressive model은 다음 결과가 이전 결과에 영향을 받는 모델을 의미하는데, train이 쉽고 빠른 prediction이 가능하게 합니다.

하지만, autoregressive model은 해석하기가 어렵고, observation이 sparse 할 때 성능이 떨어집니다.

Autoregressive model 중 한 가지로 latent variable model이 있는데, 저자들이 본 논문에서 제시하는 Latent ODE가 바로 latent variable model 중 하나입니다.

Latent ODE는 위에서 설명드린 VAE의 encoder에 ODE-RNN을 사용한 구조입니다.

ODE-RNN의 아이디어만큼이나 간단한데요, 먼저 구조를 그림으로 보여드리겠습니다.

Latent ODE model with an ODE-RNN encoder

이 모델이 prediction을 할 때, ODE-RNN encoder가 initial state의 posterior $q(z_{0}|{x_{i},t_{i}})$ 를 근사하기 위해 time을 거슬러 backward로 작동합니다.

그리고 $z_{0}$ 가 주어지면 어떤 time point든 ODE initial value problem을 풀어 latent state를 구할 수 있습니다.

Latent ODEs를 구성하는 수식은 아래와 같습니다.

$z_{0}{\sim}p(z_{0})$

$z_{0},...,z_{N}=ODESolve(f_{\theta},z_{0},(t_{0},...,t_{N}))$

$x_{i}{\sim}p(x_{i}|z_{i})$

$q(z_{0}|{x_{i},t_{i}})=N({\mu}_{z_{0}},{\sigma}_{z_{0}}) where {\mu}_{z_{0}},{\sigma}_{z_{0}}=g(ODERNN_{\phi}({x_{i},t_{i}}))$

간단히 설명해보면, 위에서 정의한 ODE-RNN을 사용해 $z_{0}$ 의 conditional distribution의 평균과 표준편차를 구합니다. 이 때 conditional distribution은 구하기 쉬운 정규분포로 가정합니다. 그리고 그 분포에서 $z_{0}$ 를 sampling 한 다음, ODE를 풀어 모든 time step에서의 $z_{i}$ 를 구하고, 그로부터 $\hat{x}_{i}$를 생성할 수 있게 됩니다.

이 논문에서는 VAE의 encoder에 ODE-RNN을 쓰고 decoder에 ODE를 썼지만, encoder와 decoder에 다양한 모델을 적용시킬 수 있습니다.

저자들이 모델의 성능 비교를 위해 사용한 baseline의 구조들은 다음과 같습니다.

Different encoder-decoder architectures

지금까지 ODE-RNN과 그것을 encoder로 사용한 Latent ODEs를 알아보았습니다. 지금부터는 두 모델의 성능을 확인해보겠습니다.

VAE의 encoder로 ODE-RNN을 사용하고, decoder로 ODE를 사용해 모든 time에 대해 latent state를 구할 수 있다!

Latent ODE vs. ODE-RNN

저자들은 autoregressive modle은 dynamics가 hidden state update에 따라 implicit하게 encode 된다고 하면서 이 점이 모델에 대한 해석을 어렵게 한다고 합니다.

반면에, Latent variable 모델은 state를 $z_{t}$ 를 통해 explicit하게 represent하고, dynamics를 generative model로 explicit하게 represent한다고 했습니다.

후에 experiment 파트에서도 Latent variable 모델이 autoregressive model보다 조금 더 좋은 성능을 내는 것을 확인할 수 있습니다.

4. Experiment

본 논문에서 저자들은 다양한 baseline과 실험을 통해 ODE-RNN과 Latent ODEs를 비교했습니다.

Experiment setup

• Dataset

  • Toy dataset (extrapolation)

  • MuJoCo (extrapolation, interpolation)

  • Physionet (time-series prediction)

  • Human Activity (time-series prediction)

• baseline

  • Autoregressive model

    1. ODE-RNN

    2. RNN

    3. RNN-Decay

    4. RNN-Impute (missing values imputed by weighted average of previous value)

    5. GRU-D (GRU-Decay)

  • Encoder-Decoder model

    1. Latent ODE

    2. RNN-VAE

    3. ODE-RNN

• Evaluation Metric

  • Mean squared error

  • AUC

  • Accuracy

Result

• Toy dataset

저자들은 1000개의 periodic trajectories를로 toy dataset을 만들었습니다.

그리고 RNN을 encoder로 쓴 Latent ODE와 ODE-RNN을 encoder로 쓴 Latent ODE로 각 trajectory의 20%를 학습시킨 뒤, 다음을 trajectory를 예측하도록(extrapolation) 했습니다.

Approximate posterior smaples

위 그림에서 확인할 수 있듯이, ODE-RNN을 encoder로 쓴 Latent ODE는 training data를 한참 넘는 구간을 periodic dynamics을 유지하면서 잘 extrapolate 합니다.

반면에, RNN을 encoder로 쓴 Latent ODE는 periodic dynamics를 잘 extrapolate 하지 못하는 것을 확인할 수 있습니다.

• MuJoco Physics Simulation

이 데이터는 어떤 물체가 껑충 뛰는 physical simulation으로 이루어져 있습니다. 각 hopper의 initial position과 velocity를 sampling 하고, 이 trajectory들은 initial state에 대한 function으로 이루어져 있습니다. 저자들은 이 데이터에 대해 interpolation과 extrapolation을 각각 진행하고, MSE를 측정했습니다.

MSE(*0.01) on the MuJoCo dataset

위 표는 각각 10, 20, 30, 50%의 observation을 주고 autoregressive 모델과 Encoder-Decoder(Latent model) 모델로 interpolation과 extapolation을 한 결과입니다.

위 표에서 볼 수 있듯이, Interpolation에서는 Autoregressive 모델의 ODE-RNN이, Encoder-Decoder 모델의 Latent ODE(ODE-RNN encoder)가 성능이 가장 좋게 나왔습니다.

Extrapolation에는 Encoder-Decoder 모델은 같은 결과가 나왔으나 Autoregressive 모델에서는 ODE-RNN 모델의 성능이 좋지 않은 것을 확인할 수 있었습니다. 이는 autoregressive model은 one-step-ahead prediction을 위해 training 되었으므로 예견된 결과라고 합니다.

주목할 것은 RNN과 ODE-RNN의 성능 차이가 데이터가 sparse해 질수록(observation이 적어질수록) 커진다는 것입니다. 이를 통해 ODE 기반 모델이 sparse한 데이터에도 더 적합하다는 것을 확인할 수 있었습니다.

저자들은 또한 latent state의 norm이 trajectory에 따라 어떻게 변화하는지도 확인했습니다.

Trajectory from MuJoCo dataset & Norm of the dynamic functions

위 그림에서 확인할 수 있듯이, Latent ODE는 data의 trajectory를 잘 따라가는 것을 확인할 수 있었습니다.

또한, Latent ODE의 norm은 trajectory가 급변할 때(hopper가 땅을 박차고 올라올 때) norm이 변하는 반면, RNN의 norm은 특별한 규칙 없이 변하는 것을 확인할 수 있었습니다.

이는 Latent ODE가 RNN보다 hidden state에 더 유의미한 정보를 담고있는 것을 의미합니다.

• Physionet

이 데이터는 8000개의 time-series 포인트로 구성되어 있고, irregular time step과 sparse한 것이 특징입니다. 여기서 저자들은 observation time에 Poisson Process likelihood를 포함시켜 Latent ODE 모델과 같이 학습시켰을 때의 성능도 확인해 봤습니다.

MSE on PhysioNet, Autoregressive models

MSE on PhysioNet, Encoder-Decoder models

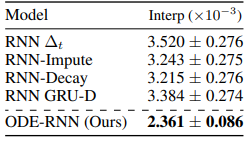
위 테이블에서 확인할 수 있듯이, Autoregressive 모델과 Encoder-Decoder 모델에서 역시 저자들의 모델이 다른 baseline보다 좋은 성능을 내고 있습니다.

• Human Activity dataset

이 데이터에는 다섯가지 activity(걷기, 앉기, 눕기 등)에 대한 time series data가 포함되어 있습니다.

Per-time-point classification, accuracy on Human Activity

이 데이터에서도 저자들의 모델의 성능이 다른 모델의 성능보다 좋은 것을 확인할 수 있었습니다.

5. Conclusion

Summary

이 논문에서는 hidden state dynamics를 Neural ODE로 구성한 ODE-RNN을 소개했습니다.

또한 이 모델을 VAE의 encoder로 사용한 Latent ODE도 제안했습니다.

이를 통해 지금까지 discrete한 hidden layer를 가졌던 모형들이 아닌, continuous한 hidden layer를 가진 모형으로서 기존 방법론들의 단점(irregular time step, sparse data에서 성능이 저하되는 현상)을 극복할 수 있었습니다.

Latent ODE는 비교적 hidden state에 대한 설명력을 가지며 observation time에 구애받지도, 전처리 과정에 data를 impute 할 필요도 없습니다.

이에 수많은 irregularly-sampled time series data에 적용 가능할 것으로 보입니다.

내 생각...

본 논문은 2018년 NeurIPS에서 best paper를 받은 Neural ODE를 RNN과 VAE에 적용시킨 후속 연구입니다.

Neural ODE라는 새로운 방식을 여러 방면에 접목시킨 논문들이 우후죽순 생겨나고 있습니다.

처음 시도되는 방법론이다 보니 특별한 theoretical contribution이 없어도 접목만 잘 시키면 논문이 publish 되기가 용이한 것 같습니다.

우리도 지금 어떤 연구가 trend인지 잘 follow up하는 자세가 필요할 것입니다.

또한 연구도 융합의 시대인 것 같습니다. 분야를 가리지 않고 여러 방법론을 창의적으로 녹여내는 것이 새로운 연구의 창을 열 수 있을 것입니다.

---

Author Information

• Wonjoong Kim

  • Affiliation: DSAIL@KAIST

  • Research Topic: GNN, NeuralODE, Active learning

  • Contact: [e-mail]

6. Reference & Additional materials

• Github Implementation

  • None

• Reference

  • Recurrent Neural Networks

  • Neural Ordinary Differential Equations

  • Variational Autoencoder

  • CS231n lecture slide