G-Meta
Kexin Huang / Graph Meta Learning via Local Subgraphs / NeurIPS-2020
1. Problem Definition
G-Meta[1]에서는 Meta-learning on graph 분야에서 local subgraphs를 활용하는 방법론을 제시한다. 저자는 왜 그래프에서 local subgraph를 활용하였는 지, 이론적 근거와 실험을 통해 제시하고 있다.
2. Motivation
Meta Learning 및 Few-shot Learning
메타러닝(Meta Learning)은 새로운 task에 대한 데이터가 부족할 때, Prior Experiences 또는 Inductive Biases를 바탕으로 빠르게 새로운 task에 대하여 적응하도록 학습하는 방법을 말한다. 'Learning to Learn'이라는 용어로 많이 설명되곤 하는 데, 대표적인 접근 방법으로는 거리 기반 학습(Metric Based Learning), 모델 기반 학습 (Model-Based Approach), 그리고 최적화 학습 방식(Optimizer Learning)이 있다. 이 중, G-Meta를 제대로 이해하기 위해서는 거리 학습 기반의 ProtoNet[2]과 최적화 학습 방식의 MAML[3]에 대한 이해가 선행되어야 한다. 이 둘을 살펴보기 전에, Few-shot Learning이 무엇인 지 먼저 짚어보고 넘어가겠다.
Few-shot Learning은 적은 데이터를 가지고 효율적으로 학습하는 문제를 해결하기 위한 학습 방법이다.
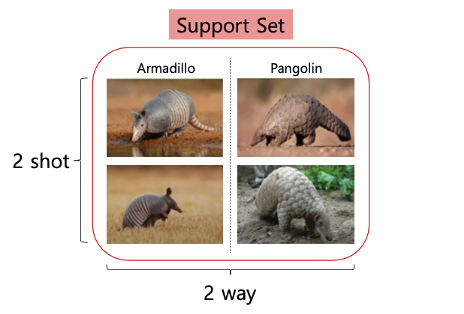
예를 들어, 위와 같이 사람에게 아르마딜로(Armadillo)와 천산갑(Pangolin)의 사진을 각각 2장씩 보여줬다고 생각해보자. 아마 대부분의 사람들은 아르마딜로와 천산갑이 생소할 것이다. 자, 이제 그 사람에게 다음의 사진을 한 장 더 보여주었다.

위 사진의 동물이 아르마딜로인지, 천산갑인지 맞춰보라고 하면, 너무나 쉽게 천산갑임을 자신있게 외칠 수 있을 것이다. 사람들은 어떻게 이렇게 적은 양의 사진을 보고도, 두 동물을 구분할 수 있는 능력을 가지게 되었을까? 사람과는 달리 기존 머신러닝(Machine Learning)은 저 두 동물을 구분하기 위해 많은 양의 사진을 보고 학습하여야 할 것이다. 만약 모델이 아르마딜로와 천산갑을 잘 구분할 수 있게 되었다고 하자. 이제 갑자기 아래 두 동물을 구분하라고 하면 어떻게 될까?
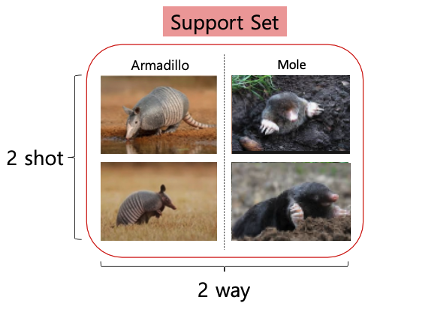
두더지(Mole)는 모델이 처음 보는 동물이기 때문에 두 동물을 구분하려면 다시 두더지에 대한 사진을 학습을 해야할 것이다. 하지만 사람은 여전히 두 동물을 쉽게 구분할 수 있다. 사람과 같이 적은 양의 사진만 보고도 Class를 구분할 수 있는 능력을 학습하는 것이 Few-shot Learning이고, 이를 학습하기 위해 Meta-Learning의 학습 방법을 활용한다.
G-Meta는 Few-shot Learning을 기반으로 학습을 하기 때문에, Label된 데이터가 적은 그래프 데이터셋에 적합한 모델을 제시하고 있다. Few-shot Learning에서 쓰이는 용어를 정리하고 넘어가면, 처음 모델에게 제시해주는 Class별 대표사진들을 Support Set이라고 한다. 2개의 Class로 구성되어 있다면 2-way라고 하며, Class별로 2장의 대표사진을 보여준다면 2-shot이라고 한다. 그리고 1장의 새로운 사진을 보여주는 데 이렇게 맞춰보라고 보여주는 사진들을 Query Set이라고 하며, 1번 맞춰보라고 주었으니 Query는 1개이다. Support Set과 Query Set을 합쳐서 하나의 Task 또는 Episode라고 지칭한다.
ProtoNet
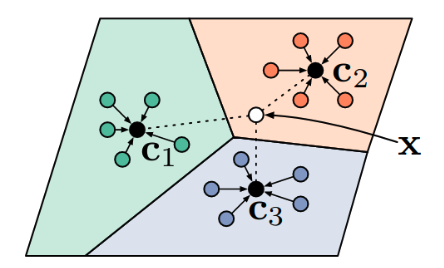
Meta Learning 방법론 중 '거리 기반 학습'의 방법은 Support Set과 Query Set 간의 거리(유사도)를 측정하는 방식이다. 그 중 대표적인 알고리즘으로 ProtoNet이 있는 데, 모델은 주어진 Support Set을 임베딩한 후, 각 Class를 대표하는 Prototype을 만든다. 그 후 Query와 Prototypes 간의 거리(유클리디안)를 기반으로 Query와 Prototype이 같은 클래스면 가깝게, 다른 클래스면 멀게 하는 방식으로 모델을 학습시킨다.
MAML (Model-Agnostic Meta-Learning for Fast Adaptation of Deep Networks)
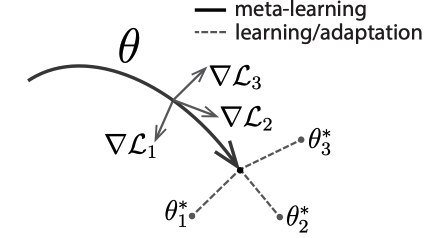
MAML은 최적화 학습 방식의 Meta Learning 방법론으로서 가장 대표적인 논문이라고 할 수 있다. 전체적인 개념은 어떤 Task에도 빠르게 적응(Fast Adaptation)할 수 있는 파라미터를 찾는 것이 이 모델의 목적이다. 일반적으로 딥러닝 모델은 기울기의 역전파를 통해 학습을 진행하나, 이런 학습 방법은 데이터가 충분히 많을 때 잘 작동하는 방식이다. 이 모델은 Task 하나하나에 대한 그래디언트를 업데이트 하는 inner loop와, 각 태스크에서 계산했던 그래디언트를 합산하여 모델을 업데이트하는 outer loop 단계로 이루어져있다(아래 그림에서의 실선). 공통 파라미터 ![]() 는 Task agnostic하게 빠르게 적응할 수 있는 파라미터이고, 다시 모델이 이 파라미터로부터 어떤 Task를 학습하게 되면 그 Task에 최적화된 파라미터를 빠르게 찾을 수 있게 된다.
는 Task agnostic하게 빠르게 적응할 수 있는 파라미터이고, 다시 모델이 이 파라미터로부터 어떤 Task를 학습하게 되면 그 Task에 최적화된 파라미터를 빠르게 찾을 수 있게 된다.
Graph Neural Networks (GNNs)
Graph 분야에서의 Meta Learning은 요즘 관심이 많아지고 있기는 하지만, Images Vision 이나 NLP 분야에 비하면 아직 활발한 연구가 이루어지지는 않고 있다. Graph가 다른 분야와 크게 다르다고 생각되는 점은 Vision에서 이루어지고 있는 데이터에 비해서 label이 굉장히 적다(sparsity)는 점과 Graph 데이터셋에는 Node와 Edge로 이루어진 Strucure가 있다는 점이다. 저자도 Graph 데이터의 Structure를 잘 잡아내는 것, 그리고 라벨이 적은 상황에서도 General한 모델을 만드는 것에 집중하고 있다.\
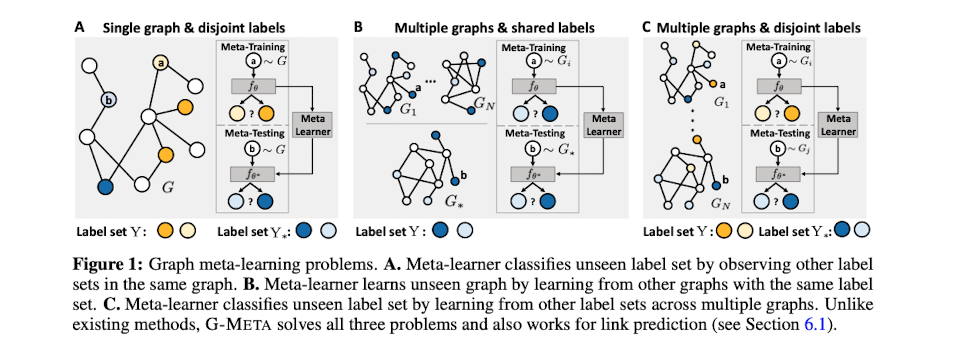
Figure 1을 보면 본 논문에서 정의한 GNN에서의 Meta Learning Task는 3가지이다.
A. Single graph & disjoint labels : '같은 그래프 내에서, label sets(노란색)를 구분하는 능력'으로, 처음 보는 label sets(파란색)들을 구분하는 task
B. Multiple graphs & shared labels : '다른 그래프들에서, labels sets(파란색)를 구분하는 능력'으로, 처음 보는 그래프에서도 그 labels sets(파란색)을 구분하는 task
C. Multiple graphs & disjoint labels : '다른 그래프들에서, labels sets(노락색)를 구분하는 능력'으로, 처음 보는 그래프에서 처음 보는 labels sets(파란색)을 구분하는 task
기존 모델들은 보통 위의 3가지 Task 중 1개의 Task에만 집중하고 있는 반면, G-Meta는 3가지 Task 모두에 대해서 자신감 있게 서술하고 있다.
Local Subgraphs and Theoretical Motivations for G-Meta
저자는 local subgraph가 전체 그래프에서의 주요한 정보를 잘 보존하고 있다고 주장하고, 이론적 정당성을 서술하고 있다.
먼저 Local Subgraph가 전체 그래프의 정보를 얼마나 보존할 수 있는 지를 증명한다. 논문에서는 수식이 가득하나, 본 리뷰에서는 수식 하나하나 뜯어보는 것보다 어떤 전개로 증명을 하고 있는 지 정리하였다. 그 전에 필요한 정의는 다음과 같다.



[5] Loss support Support set 내 Centroid Embeddings들과 Prototype과의 Euclidean distance를 계산하여 class distribution vector p를 계산한다. 그리고 Cross-entropy loss를 계산한다.
Theorem 1

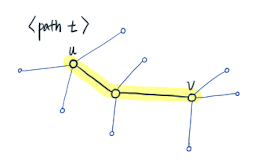
Node Influence
는
과 같이 정의되는데, 위 그림에서의
는 shortest path distance가 2이다. 이 때
가 커지면, 다시 말해 두 노드간의 거리가 멀어지면 그 노드들의 Influence는 exponential하게 감소한다.
두 노드 사이의 Path에 속한 노드들의 degree가 높을수록, 두 노드간의 influence가 줄어든다.
우리가 사용하는 그래프 데이터들은 주로 복잡하고, 상대적으로 노드들의 degree가 높다.
따라서 거리가 먼 두 노드들은 서로에게 미치는 influece가 현저히 낮다.
결론적으로 특정 노드의 Local Subgraph에는 그 노드를 표현하는 주된 정보를 가지고 있기 때문에, 굳이 노드를 GNN으로 표현하기 위해 전체 그래프를 볼 필요가 없다.
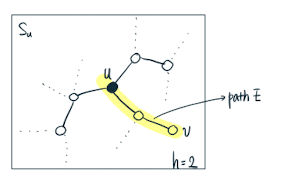
Theorem 2
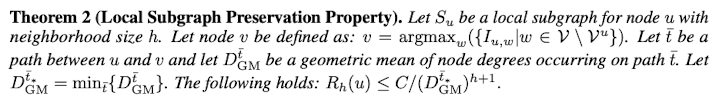
위의 그림 2-hop에 속하는 subgraph 내 Node들 중에서 Node u와 Influence가 최대인 Node를 Node v라고 하였을 때, Graph influence loss
과 같다.
Graph Influence loss는 h가 늘어날수록, 즉 노드 간의 거리가 멀어질수록 exponential하게 감소한다.
즉, graph influence loss는 h에 의해 decaying term으로 작용하고, local subgraph formulation은 전체 그래프의 GNN에 대한
order approximation이라고 볼 수 있다.
상기 서술한 이론적 근거를 바탕으로 local subgraphs는 어떤 Node를 Representation할 때 필요한 충분한 정보가 담겨 있는 것을 알 수 있다. 이와 더불어 local subgraph를 활용했을 때 다음과 같은 장점이 있다.
Structures : 그래프의 전체 구조를 활용하면 크기가 너무 크기 때문에 기존의 GNN으로는 그래프의 Structure 정보를 담아내기 어려웠다. 하지만 크기가 작은 Local Subgraphs를 이용함으로서 노드의 정보가 적은(sparse)한 환경에서, Structure의 정보를 충분히 활용할 수 있기 때문에 모델에게 유용한 정보로 작용한다.
Features : Local Subgraphs는 상기 Theorem에서 증명한 것처럼 주요한 정보를 잘 담고 있다.
Labels : 일반적으로 그래프에는 소량의 라벨만 되어있기 때문에 전체 그래프에서 라벨에 대한 정보를 효율적으로 propagate하기 어렵지만, local subgraph는 크기가 작기 때문에 Label의 정보를 propagation하기에 용이하다.
3. Method
Local Subgraph를 사용한다는 이론적 정당성을 갖췄으므로, 이제 G-Meta의 Methodology에 대해서 상세히 살펴본다. G-Meta의 Architecture는 사실상 MAML[2]과 ProtoNet[1]을 Subgraph를 활용하여 합쳐놓은 것이라고 보면 간단하다.
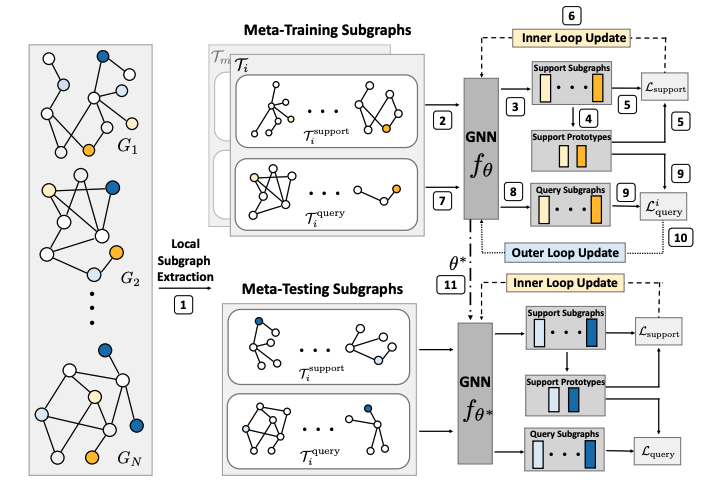
[1] Local Subgraph Extraction 먼저 각 노드들마다 h-hop의 subgraph를 생성한다. 본 논문에서는 2~3hop이 좋은 성능을 보인다고 한다. 그렇게 각 노드마다 Subgraph를 만들면, 기준이 되는 노드를 'centroid node'라고 지칭한다. Subgraph로 표현된 노드들을 샘플링하여 Meta-Training과 Meta-Testing에 필요한 Task를 generation한다.
[2][3] Support Set Embeddings Support set을 GNN을 이용하여 임베딩한다. Subgraphs를 이용하여 centroid 노드를 임베딩하는 것으로 Centroid node embedding이라고 지칭하고 있다.
[4] Build Prototypes 임베딩된 Centroid 노드들 중에 같은 Label을 공유하는 노드들끼리 Mean을 취하여 Prototype을 생성한다.
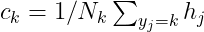
[5] Loss support Support set 내 Centroid Embeddings들과 Prototype과의 Euclidean distance를 계산하여 class distribution vector p를 계산한다. 그리고 Cross-entropy loss를 계산한다.
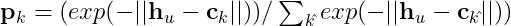
[6] Inner Loop Update 각 태스크에 대해서 GNN parameter를 SGD으로 update한다.
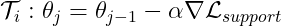
[7][8] Query Set Embeddings Query Set을 Support set을 이용하여 update 시킨 GNN을 이용하여 임베딩 시킨다.
[9] Loss query Query Set의 Centroid Embeddings들과 4)에서 만든 Prototype과의 Euclidean distance를 기반으로 Cross-entropy loss를 계산한다.
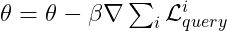
[10] Outer Loop Update
Loss support와는 다르게 각 Task에 대해 GNN을 update하는 것이 아니라, 모든 tasks에 대한 loss를 모두 합한 후에 한 번에 Update 시킨다. 이는 MAML의 학습 방법과 같다. 다른 batch에 속한 tasks들에 대해서도 1)~10)과정을 반복하여 GNN을 학습시킨 후, 학습이 끝난 GNN의 파라미터 ![]() 는 새로운 task들에 대해서 몇 번의 update만으로도 빠르게 적응할 수 있는 파라미터이다.
는 새로운 task들에 대해서 몇 번의 update만으로도 빠르게 적응할 수 있는 파라미터이다.
[11] Meta-Test 새로운 task에 대해서 빠르게 적응하기 위해서, Meta-test set의 task들을 ![]() 파라미터를 초기값으로 수 번의 Update를 추가적으로 진행한다. 이런 과정을 통해 unseen tasks들까지 generalization을 할 수 있는 Meta-learned 모델을 만들 수 있다.
파라미터를 초기값으로 수 번의 Update를 추가적으로 진행한다. 이런 과정을 통해 unseen tasks들까지 generalization을 할 수 있는 Meta-learned 모델을 만들 수 있다.

4. Experiment
Experiment setup
Dataset
실험에 쓰인 데이터셋은 다음과 같다.
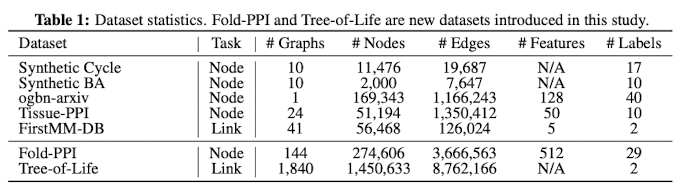
baseline
Meta-Graph : VGAE를 활용하여 few-shot multi-graph link prediction을 하는 모델 Meta-GNN : MAML을 Graph에 접목시킨 모델
FS-GIN : Few-shot Graph Isomorphism Network로서 GIN을 전체 그래프에 적용시키고, few-shot setting에 접목시킴
FS-SGC : FS-GIN에서 GIN을 SGC로 교체한 모델
No-Finetune : 각 데이터셋에서 성능이 가장 좋은 모델을 support set으로 training을 시킨 후 바로 Finetuning 없이 바로 query set을 classify
KNN : Train된 GNN을 활용하여 support set을 임베딩 한 후, query set과 K-closest한 support set을 바탕으로 Prediction
Finetune : 각 데이터셋에서 성능이 가장 좋은 모델을 Meta-training set으로 GNN을 학습시킨 후, Meta-testing set으로 finetuning한 모델
ProtoNet : Subgraph embeddings으로 Prototypycal Learning만 한 경우 (MAML의 구조가 빠졌다고 생각하면 된다.)
MAML : Prototypical Loss가 빠졌다고 생각하면 된다.
ProtoNet과 MAML은 각각 G-Meta에서 주요한 baselines으로서 G-Meta의 ablation study를 한 것이라고 보면 된다. ProtoNet은 MAML구조를, MAML은 Prototypical Loss를 없앤 실험이다.
Evaluation Metric
Node Classification
Disjoint label settings
meta-testing, meta-validation에 쓰일 라벨을 5개씩 할당하고, 나머지는 모두 meta-training에 쓰였다.
dataset
way
shot
num of update in meta-training
num of update in meta-testing
Synthetic Cycle
2
1
5
10
Synthetic BA
2
1
5
10
ogbn-arxiv
3
3
10
20
Tissue-PPI
3
3
10
20
FirstMM-DB
3
3
10
20
Fold-PPI
3
3
10
20
Tree-of-Life
3
3
10
20
Multiple graph shared labels settings
전체 그래프의 10%가 testing(validation)에 쓰이고, 나머지는 모두 Training하는 데 쓰였다.
Link prediction
그래프의 10%/10%가 각각 testing과 validation에 쓰였다. 각 그래프마다 support set/query set을 30%/70%의 edges로 구성하였다. Negative edges는 Positive edges의 수를 맞추기 위해 같은 개수만큼 랜덤으로 샘플링하였다. 각 task마다 16개의 Shot을 사용하였다 (32 Node pairs). meta-training에서는 10번의 gradient update를 하였고, meta-testing에서는 20번의 gradient update를 진행하였다.
Result
Graph meta-learning performance on synthetic datasets
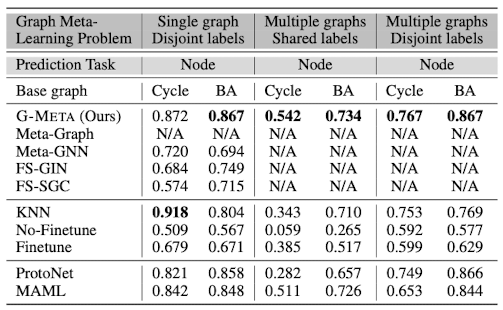
Graph meta-learning performance on real-world datasets
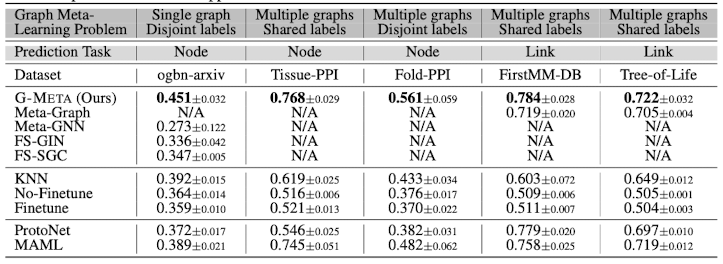
실험 결과에서 해석할 수 있는 G-Meta의 Contribution은 다음과 같다.
Synthetic datasets은 nodes' structural roles에 의해서 라벨이 결정되는 데이터셋으로, G-Meta가 local graph structure를 잘 잡아내는 지 확인하기 위한 실험에 쓰였다. Synthetic datasets의 결과에서, Meta-GNN, FS-GIN, FS-SGC와 같이 전체 그래프 구조를 기반으로 하는 모델들에 비해 Subgraph 기반의 모델들이 더 성능이 좋다는 것을 볼 수 있는데 이를 통해 subgraphs가 local structural roles을 잘 잡아낸다는 것을 내포하는 실험 결과라고 볼 수 있다.
Single graph disjoing labels, multiple graphs shared labels, multiple graphs disjoint labels와 같은 다양한 task들에 대해서 general하게 좋은 성능을 보여주고 있다.
labels set가 공유되지 않은 상황에서도 G-Meta는 subgraph를 통해 transferable signal을 학습할 수 있다.
5. Conclusion
Summary
Scalability : 전체 그래프를 활용하는 것이 아니라, subgraph만 사용을 하기 때문에 Scalable하다.
Inductive Learning : 각 노드마다 다른 subgraph를 활용하여 Centroid Embeddings을 하기 때문에 Inductive하다.
Over-smoothing regularization : GNN에서 대표적으로 문제가 되는 것은 connected nodes들이 interation을 거칠수록 over-smoothing이 되는 것이다. 하지만 G-Meta에서는 다양한 structures를 가진 subgraphs들을 이용하기 때문에 over-smoothing을 예방할 수 있다고 한다.
Few-shot Learning : 적은 양의 데이터를 활용하는 Few-shot Learning의 방법을 채택했기 때문에, sparse한 그래프 데이터에서 학습이 유리하다.
Graph Meta Learnings에서 가능한 다양한 tasks(3가지)에 적용 가능하다.
Discussion
G-Meta는 Meta-learning과 few-shot learning에서 대표적인 논문이라고 할 수 있는 MAML과 ProtoNet을 결합시키는 동시에, Node를 subgraph를 활용하여 임베딩 시키는 방법론을 제시하였다. 방법론 자체로만 본다면 Novelty가 크진 않다고 볼 수 있으나, subgraph를 활용하는 것에 대한 이론적 근거를 뒷받침하고, 다양한 데이터셋과 실험을 통해 타당성을 더 탄탄하게 입증하였다. Meta-learning on graph를 다룬 논문이지만, Subgraph가 어떤 의미를 가지고 있고, 어떠한 장점들을 (scalable, inductiveness 등) 가지고 갈 수 있는 지에 대한 Insight를 제시한 점이 본 논문의 key takeaway라고 생각한다.
Author Information
김성원 (Sungwon Kim)
Graph Neural Network, Meta-Learning, Few-shot Learning
6. Reference & Additional materials
https://github.com/mims-harvard/G-Meta
Reference [1] Huang, Kexin, and Marinka Zitnik. "Graph meta learning via local subgraphs." Advances in Neural Information Processing Systems 33 (2020): 5862-5874. [2] Snell, Jake, Kevin Swersky, and Richard Zemel. "Prototypical networks for few-shot learning." Advances in neural information processing systems 30 (2017). [3] Finn, Chelsea, Pieter Abbeel, and Sergey Levine. "Model-agnostic meta-learning for fast adaptation of deep networks." International conference on machine learning. PMLR, 2017.
Last updated