GRAND

Chamberlain & Rowbottom et al. / GRAND_Graph Neural Diffusion / ICML-2021

논문 링크

Official Github

본 포스팅이 잘 안 보이는 경우, 블로그에서 확인해주세요.

1. Problem Definition

본 논문은 그래프 신경망(Graph Neural Network; GNN)의 메세지 전달 방식을 편미분 방정식(partial differential equation; PDE) 형태의 확산 방정식(diffusion equation)으로 해석해, 그래프 학습에서 발생하는 여러 가지 문제(e.g. 얕은 구조, oversmoothing, bottleneck)를 다루는 새로운 방식의 GNN을 제안합니다.

본 논문에 대한 본격적인 설명에 들어가기 앞서, 본 논문과 관련된 개념 및 문제들을 간단히 정리해보도록 하겠습니다.

1-1. 편미분 방정식(PDEs)

위키피디아1에서는 편미분 방정식을 다음과 같이 설명하고 있습니다.

수학에서, 편미분 방정식(PDE)은 여러 개의 독립 변수로 구성된 함수와 그 함수의 편미분으로 연관된 방정식이다. 각각의 변수들의 상관관계를 고려하지 않고 변화량을 보고 싶을 때 이용할 수 있으며, 상미분방정식에 비해 응용범위가 훨씬 크다. 소리나 열의 전파 과정, 전자기학, 유체역학, 양자역학 등 수많은 역학계에 관련된 예가 많다.

본 논문에서 GNN의 메시지 전달 방식을 모델링할 때 사용되는 열 확산 방정식은 어떤 시간 에서의 입자의 위치 등의 두 변수를 가지므로 편미분 방정식으로 표현됩니다.

1-2. 확산방정식

확산(diffusion)이란 밀도가 높은 지역에서 밀도가 낮은 지역으로 물질이 이동하는 것을 의미합니다. 예를 들어, 차가운 표현에 위치한 뜨거운 물체가 있을 때, 열은 물체에서 표면으로 두 온도가 같아질 때까지 확산됩니다.

먼저, 는 어떤 시간 에서 어떤 위치 위의 물체가 가지는 어떤 특성 (편의를 위해 온도로 가정)의 분포를 나타내는 )의 scalar-valued 함수족(family)라고 정의하고, 는 시간 에서 어떤 위치 에서의 그 값이라고 정의해봅시다. 푸리에의 열전도 법칙(Fourier's law of heat conduction)에 따라 열유속(heat flux)은 아래와 같이 온도의 그라디언트(gradient) 와 의 열전도(thermal conductance) 특성으로 표현될 수 있는 확산률(diffusivity) 에 비례합니다.

$h = -g \nabla x$

확산률 는 전체에 걸쳐 균일할(homogeneous) 경우 스칼라 상수로 표현됩니다. 만약 위치에 따라 분균일할 (inhomogeneous)할 경우, 그림 12과 같이 scalar-valued 함수(isotropic) 또는 matrix-valued 함수(anisotropic)로 표현됩니다.

그림 1 - Inhomogeneous Diffusivity

연속성 조건 을 통해 PDE 형태의 열 확산 방정식(heat diffusion equation)을 유도할 수 있습니다.(유도과정은 생략합니다. 관심있으신 분들은 "Advanced Engineering Mathematics by Erwin Kreyszig" 등을 참고하세요 살려줘...)

$\frac{\partial x(u, t)}{\partial t} = \text{div}[g(u, x(u,t), t) \nabla x(u,t)]$

$\text{initial condition: }x(u,t) = x_{0}(t)$

div: divergence3, 즉 벡터장에서 정의되는 미분연산자

따라서, 균일한 diffusivity를 갖는다고 가정할 때, 열확산 방정식을 다음과 같이 나타낼 수 있습니다.

$\frac{\partial x(u, t)}{\partial t} = \text{div}(c \nabla x) = c \Delta x$

이 때 로 Laplacian operator 라고 합니다.

이 식의 의미를 해석4해보면,

• 2차 미분계수(즉, 변곡점)가 클수록 (볼록할수록) 온도의 변화는 더 빨리 일어난다.

  • 주변과 온도 차가 클수록 온도가 더 빨리 변화한다. 온도 변화의 속도를 의미

• 위로 볼록(2차 미분계수 < 0)하면 온도가 떨어지고, 아래로 볼록(2차 미분계수 > 0) 하면 온도가 올라간다.

  • 온도 변화의 부호를 의미

즉, 열 확산 방정식은 주변 온도가 높을 수록 온도는 빨리 올라가고, 주변 온도가 낮을 수록 온도가 빨리 내려가는 것을 수학적으로 표현한 것입니다.

이 후 Motivation 각 미분연산자(e.g. gradient, divergence, Laplacian operator)가 그래프에서 어떻게 정의될 수 있는지와 더불어 GRAND는 Diffusivity를 어떻게 활용하는지를 살펴보겠습니다.

2. Motivation

2-1. 그래프 학습에서 발생하는 여러 가지 문제

• 얕은 구조 (Depth)와 Oversmoothing5: Oversmoothing은 GNN의 layer의 수(Depth)가 증가할수록 노드의 embedding이 점점 유사해지는 현상을 말합니다. 이로 인해, 대부분의 GNN은 깊은 신경망을 쌓지 못하고, 얕은 구조를 가지게 됩니다.

그림 2 - GCN 1,2,3,4,5 layer를 통해 얻은 Zachary’s karate club network data의 노드 Embedding

• Bottleneck과 Over-squashing6: Bottleneck은 GNN의 layer가 증가할수록 기하급수적으로 늘어나는 정보를 고정된 크기의 벡터로 압축(squashing)시키는 것을 의미하며, 이로 인해 먼 거리의 노드와의 메세지 전달을 용이하지 못하게 만드는 현상을 의미합니다.

그림 3 - GNN에서의 Bottleneck & Over-squashing

2-2. 그래프에서의 확산 방정식

본 논문은 그래프의 메세지 전달 방식을 열 확산 방정식으로 모델링해 PDE를 풀어냄으로써, 연속적인 layer를 구성해 깊은 모델 을 쌓을 수 있는 Neural ODE/PDE의 이점을 그래프로 확장시키려는 시도를 하고 있습니다. 이를 통해 앞서 서술한 그래프 학습의 고질적인 문제들을 해결하는 새로운 GNN(GRAND)을 제안합니다.

이를 위해, 열 확산 방정식의 미분연산자들을 그래프에서 새롭게 정의할 필요가 있습니다. 본 논문에서의 수식 표기법은 편의를 위해 vector-field를 scalar-field로 가정해 전개해 나가지만, 이것이 오히려 혼동을 야기하므로 이러한 가정을 배제하고 서술하고자 합니다(이러한 표기법은 ICLR-2022에서 발표된 GRAND++7를 참고하였습니다).

2-2-1. Notation

• 무방향 그래프(undirected graph):
• 노드(node) 수:
• 노드 특징(feature) 행렬:

  • 노드 특징 행렬의 내적은 일반적인 행렬의 내적과 같습니다. $\langle \mathbf{X}, \mathbf{Y} \rangle =Tr(\mathbf{X}^{\intercal} \mathbf{Y})=\sum_{i=1}^{n}{\mathbf{x}^{(i)} \mathbf{y}^{(j)}}$

  

  그림 4 - Matrix Inner Product

• 간선(edge) 수:
• 간선 가중치(weight) 행렬(인접 행렬과 유사):

  • 무방향 그래프이므로
  • self-edge가 없음 (i.e. )
  • 
• 간선 특징(feature) 텐서:

  • $\mathfrak{X} = \begin{bmatrix} \mathcal{X}^{(1,1)} & \cdots & \mathcal{X}^{(1,n)}\\ \vdots & \ddots & \vdots\\ \mathcal{X}^{(n,1)} & \cdots & \mathcal{X}^{(n,n)} \end{bmatrix} \in \mathbb{R}^{n \times n \times k}$

  • 
  • 간선 특징 텐서의 내적은 다음과 같이 정의합니다. 여기서 1/2은 무방향 그래프이므로 중복된 합을 피하기 위해 사용(본 논문에서는 upper triangle matrix만 더하는 방향으로 표기: ), 는 간선의 유무를 나타내기 위한 indicator로 사용한 것으로 보입니다. $\langle \langle \mathfrak{X}, \mathfrak{Y} \rangle \rangle = \frac{1}{2} \sum_{i,j=1}^{n}{w_{ij} \mathcal{X}^{(i,j)} \mathcal{Y}^{(i,j)}}$

2-2-2. 미분연산자 (Differential Operator)8

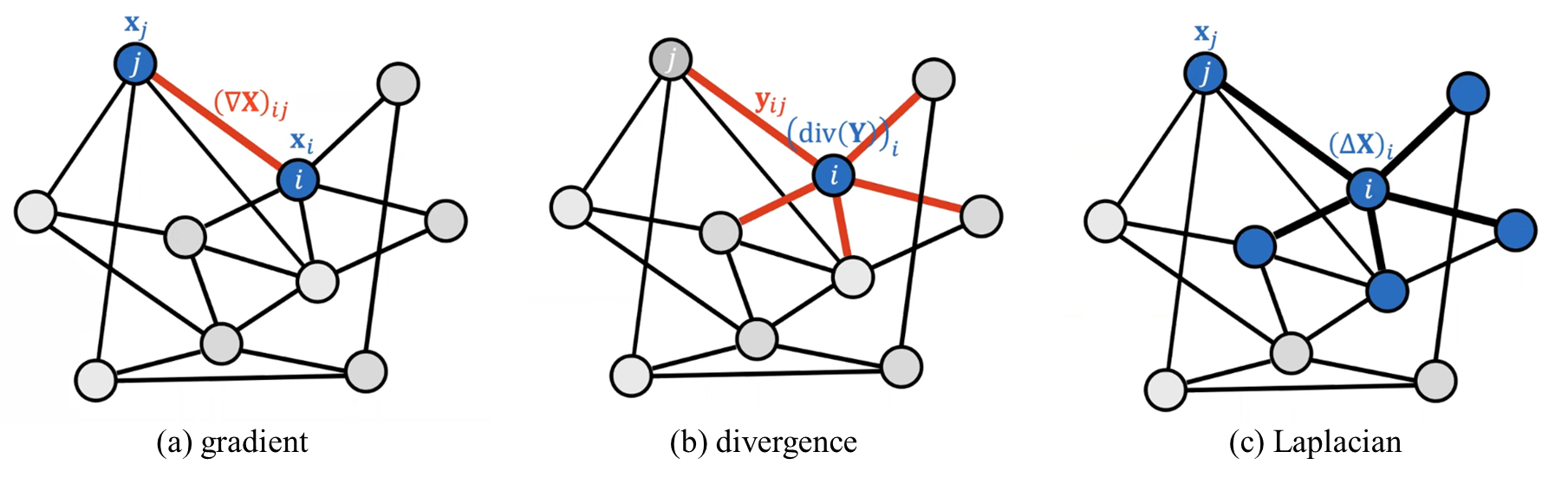
그림 5 - Differential Operators on Graph

• 그라디언트(gradient) 는 간선 에 할당
• 발산(divergence) 은 노드 i와 연결된 모든 간선의 특징의 합이 해당 노드에 할당:

  • $(\text{div}(\mathfrak{X}))_{i}=\sum_{j:(i,j) \in \mathcal{E}}{\mathcal{X}_{ij}}=\sum_{j=1}^{n}{w_{ij}} \mathcal{X}_{ij}$

• 라플라시안(Laplacian)

2-2-3. 그래프에서의 열확산 방정식[7]

먼저, 우리는 아래의 열확산 방정식을 얻을 수 있습니다.

$\frac{\partial \mathbf{X}(t)}{\partial t}=\text{div}[\mathbf{G}(\mathbf{X}(t), t) \odot \nabla \mathbf{X}(t)]$

여기서, 은 Hadamard product (i.e. element-wise 곱)으로 정의됩니다. 갑자기 Hadamard product이 등장한 이유는 gradient의 결과가 3d tensor가 되고, divergence는 벡터장에서 정의되는 미분연산자이기 때문입니다. 행렬 는 right-stochastic(즉, 각 행의 합이 1)인 와 같은 형태를 선택합니다(노드 간에 이동하는 정보가 사라지거나 생겨나지 않게 하기 위해 right-stochastic 행렬을 도입하는 것으로 보입니다). 가장 단순한 케이스를 위해 가 초기 노드 특성 에만 영향을 받는다고 가정하면 (i.e. 는 time-invariant하고, right-stochastic하다), 이는 for all 의미합니다. 그러므로 우리는 , 인 상황을 살펴보겠습니다.

이 때, 로 두면, 선형 확산 방정식을 얻을 수 있고 이 방정식의 해석적 해를 다음과 같이 얻을 수 있습니다.

$\mathbf{X}(t)=e^{\mathbf{\bar{A}}t}\mathbf{X}(0)$

이를 테일러 급수로 근사한 것이 heat kernel PageRank라고 볼 수 있습니다.9, 10

저자들은 발표한 Youtube 영상에 따르면, GRAND와 PageRank의 유사성 및 차이점을 아래와 같이 언급했습니다.11

This idea that you can also have diffusion in a completely discrete domain and in that case the most common example is probably Google's PageRank and the formulation that we're most familiar with from the gnn community is multiplying laplacian by some sort of feature matrix.

이러한 기본적인 형태를 확장해 본 논문에서는 diffusivity를 attention matrix로 가정하여, 아래와 같은 수식을 도출합니다.

그림 6 - Diffusion Equation on Graph

2-2-4. 그래프 열확산 방정식의 풀이

Explicit schemes. Forward Euler discretization: (는 discrete time index(iteration #layers)이고, 는 시간의 step size입니다.)

$\frac{\mathbf{x}_{i}^{(k+1)} - \mathbf{x}_{i}^{(k)}}{\tau}=\displaystyle\sum_{j:(i,j) \in \mathcal{E}} {a(\mathbf{x}_{i}^{(k)}, \mathbf{x}_{j}^{(k)})(\mathbf{x}_{j}^{\textcolor{red}{(k)}} - \mathbf{x}_{i}^{(k)})}$

$\Leftrightarrow \mathbf{X}^{(k+1)} = ((1-\tau)\mathbf{I} + \tau \mathbf{A}(\mathbf{X}^{(k)})) \mathbf{X}^{(k)}=\mathbf{Q}^{(k)} \mathbf{X}^{(k)}$

여기서, 의 정규화를 가정하므로, 우리는 위의 수식을 더 간단히 표현할 수 있습니다. 또한, 일 때, diffusivity는 attention이 되므로 위의 수식은 nonlinearity가 없는 GAT와 같게 됩니다.

Semi-Implicit scheme. Backward Euler discretization

$\frac{\mathbf{x}_{i}^{(k+1)} - \mathbf{x}_{i}^{(k)}}{\tau}=\sum_{j:(i,j) \in \mathcal{E}} {a(\mathbf{x}_{i}^{(k)}, \mathbf{x}_{j}^{(k)})(\mathbf{x}_{j}^{\textcolor{red}{(k+1)}} - \mathbf{x}_{i}^{(k)})}$

$\Leftrightarrow ((1-\tau)\mathbf{I} + \tau \mathbf{A}(\mathbf{X}^{(k)})) \mathbf{X}^{(k+1)} = \mathbf{X}^{(k)}$

$\Leftrightarrow \mathbf{B}^{(k)} \mathbf{X}^{(k+1)}=\mathbf{X}^{(k)}$

여기서, 는 dense하기 때문에 multi-hop filter로 해석할 수 있습니다. (다만, implicit scheme에서의 는 1-hop 인접행렬과 같은 sparsity를 구조를 가진다는 점에서 차이가 있습니다)

2-3. Discriminative Idea

본 논문은 PDE 기반의 열확산 방정식을 GNN에서의 메세지 전달 방식으로 확장시켜, 내적 및 미분연산자를 정의해 continuous한 layer를 구성할 수 있는 Neural ODE12의 이점을 활용해 그래프 학습에서 발생할 수 있는 여러 가지 문제를 해결하였습니다.

3. Method

본격적으로 논문에서 제안하는 Graph Neural Diffusion(GRAND) 방법론에 대해 논의해보겠습니다. 기본적으로 앞서 언급했던 표기법 및 그래프 확산 방정식을 따라 GRAND를 다음과 같은 문제로 정의합니다.

• Initial condition:
• 그래프 확산 방정식:
• Output:

이 때, 와 diffusivity()는 학습할 수 있는 함수입니다. 특히 diffusivity 함수는 time-invariant diffusivity 함수로 모든 layer에 걸쳐 같은 parameter를 공유합니다.

이 diffusivity는 attention 함수로 모델링되고, 실험적으로, GAT의 attention보다 일반적인 attention(scaled dot product attention13)이 더 좋은 성능을 보여, 이를 사용했습니다.

$a(\mathbf{X}_{i}, \mathbf{X}_{j})=\text{softmax} \left( \frac{(\mathbf{W}_{K} \mathbf{X}_{i})^{\intercal} \mathbf{W}_{Q} \mathbf{X}_{j}}{d_k} \right)$

여기서, 와 는 학습가능한 행렬이고, 는 의 차원을 결정짓는 hyperparameter입니다. 또한 안정적인(stabilize) 학습을 위해 multi-head attention (기대값)을 사용했습니다: . 이러한 attention weight 행렬 은 right-stochastic을 따릅니다. 따라서 그래프 확산 방정식을 다음과 같이 표현될 수 있습니다.

Attention weight 행렬을 정의하는 방식과 이를 활용하는 방식에 따라 3가지 변형 모델을 만들 수 있습니다.

• grand-l:
• grand-nl: 식 (1)과 동일

• grand-nl-rw: 식 (1)에서 간선을 로 새롭게 정의해 재연결(rewiring)한 것

  • $\mathcal{E^{'}} = \{ (i,j) : (i, j) \in \mathcal{E} \text{ and } a_{ij} \lt \rho \} \text{, where threshold } \rho$

  • 위의 조건에 따라 self-loop를 포함 가능

  • Diffusion 과정에서 a는 계속 변화하므로, 재연결(rewiring)은 의 시점에 특성값에 근거해 한 번만 시행

GRAND는 모든 layer/iteration에 걸쳐 parameter를 공유하므로 기존의 GNN 모델보다 data-efficient 하다고 볼 수 있습니다.

4. Experiment

본 논문은 아래와 같은 연구 문제에 답하기 위해 여러 가지 실험을 진행하였습니다.

1. Are GNNs derived from the diffusion PDE competitive with existing popular methods? (확산 PDE를 통해 도출된 GNN은 다른 경쟁 모델에 비해 좋은 성능을 내는가?)

2. Can we address the problem of building deep graph neural networks? (깊은 그래프 신경망 모델을 수립하는데 있어 발생하는 문제들을 해결하고 있는가?)

3. Under which conditions can implicit methods yield more efficient GNNs than explicit methods? (Implicit 방법은 어떤 상황에서 explicit 방법에 비해 좋은 성능을 내는가?)

4-1. Node Classification

표 1 - Data Summary

노드 분류에 대한 실험을 위해 위의 표와 같이 7개의 데이터셋에 대해 실험했고, 베이스라인 모델로는 아래와 같이 7개 모델을 선정했습니다. 데이터셋 및 베이스라인 모델에 대한 자세한 내용은 본 논문을 참고 부탁 드립니다.

• 대표적인 GNN: GCN, GAT, Mixture Model Networks, GraphSage

• ODE-based GNN: Continuous Graph Neural Networks(CGNN), Graph Neural Differential Equations(GDE), Ordinary Differential Equations on Graph (GODE)

• Linear Diffusion PDE: LanczosNet의 2개의 변형

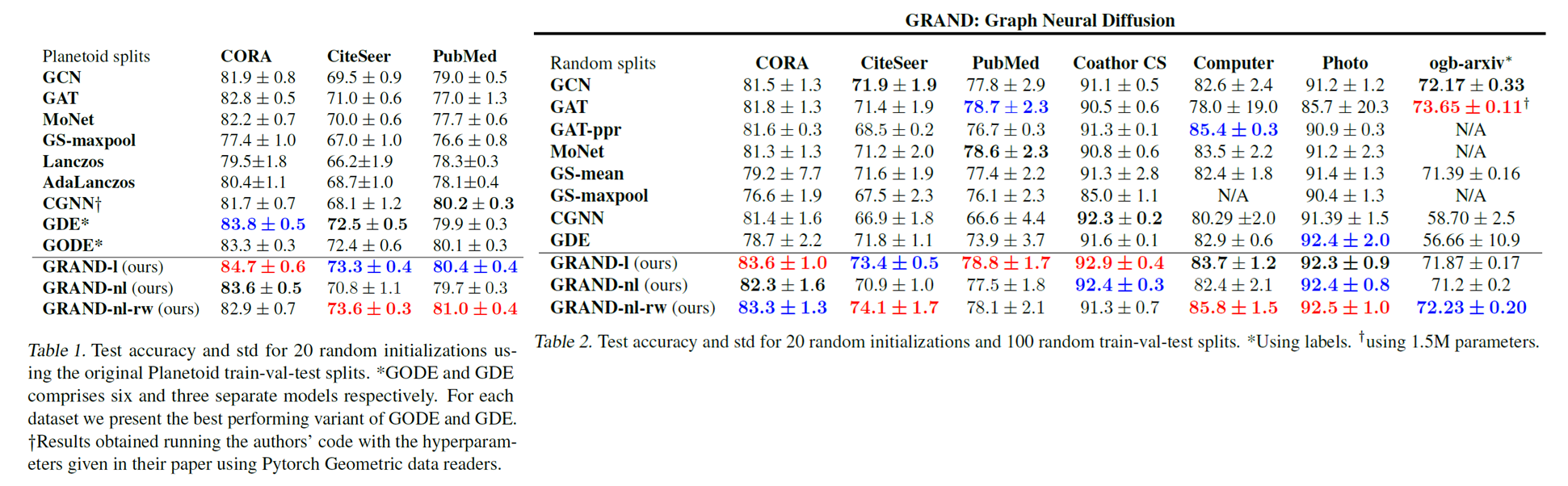
그림 7 - Node Classification Results (Planetoid/Random split)

위의 실험 결과를 통해 볼 수 있듯이, GRAND 모델들이 다른 모델들에 비해 한결같이 좋은 성능을 보였습니다. 큰 그래프인 ogb-arxiv 데이터셋에서는 GAT가 가장 좋은 성능을 보였으나, 이는 GRAND보다 20배 많은 parameter를 사용하기 때문입니다.

4-2. Depth

그림 8 - Depth

이번 실험에서는 GRAND가 깊은 그래프 신경망을 수립했음에도 불구하고, oversmoothing 문제를 해결했는지 살펴보겠습니다. 이를 위해, 다른 hyperparameter는 고정한채로 적분 구간(시간) 를 변경해 정확도(accuracy)를 측정했습니다. 위의 결과를 통해 볼 수 있듯이, GCN과 residual connection을 적용한 GCN 모델과 비교했을 때 GRAND는 layer 수가 많을 때도 성능을 유지하는 것을 확인할 수 있습니다.

4-3. Choice of discretisation scheme

그림 9 - Different Solver Effects

이번 실험은 discretisation scheme의 안정성을 보기 위해 Cora 데이터셋을 사용했습니다. PDE를 푸는데 있어 step size와 계산 시간은 trade-off관계를 갖습니다. Scheme은 아래와 같은 방법론을 사용하였고, 이에 대한 설명은 본 논문의 범위를 넘어서므로 생략합니다.

• Explicit scheme: Adams-Bashford method

• Implicit scheme: Adams-Moulton method

• Adaptive scheme: Runge-Kutta 4(5)

Method Choice. 그림 9의 왼쪽 그래프를 통해 볼 수 있듯이, explicit 방법은 작은 step size()를 제외하고는 불안정한 성능을 보이는 반면, implicit 방법은 모든 step size에서 안정적인 성능을 보입니다. 게다가 implicit 방법은 state-of-the-art 모델인 adaptive 방법에 비해 빠르게 수렴합니다. 다만, 모든 step size에 대해서 그러한 현상이 관찰되는 것은 아니며, step size가 커질수록 implicit 해는 점점 더 풀기 어려워지기 때문에 더 많은 iteration을 필요로 합니다.

Graph rewiring. 이 실험에서는 Cora 그래프를 rewiring하고, 각 노드에 대해 가장 큰 계수(#layers)를 고정하여 실험했습니다. 의 변화를 통해 sparsity, 계산 시간, 정확도(accuracy) 사이 trade-off를 확인할 수 있습니다. 그림 9의 오른쪽 그래프를 통해 볼 수 있듯이, 가 작을수록(그래프가 sparse할수록) 모든 방법론에서 더 빠르게 수렴합니다. 특히 implicit 방법에서 step size에 관계 없이 이러한 sparsification의 이점이 잘 관찰됩니다. 따라서 sparse한 그래프는 해를 푸는 어려움을 줄이는데 도움을 준다고 가정할 수 있습니다.

4-4. Diffusion on MNIST Image Data Experiments

그림 10 - MNIST Image Data Experiments

GRAND의 학습된 diffusion의 특성을 살펴보기 위해 MNIST 픽셀 데이터의 superpixel representation을 구성하는 실험을 진행했습니다. superpixel을 구성한다는 것은 인접한 패치들을 간선으로 연결하고, 이를 숫자 또는 배경으로 이진 분류하는 것을 의미합니다. 이 때 50%의 training mask를 사용합니다. Attention weight는 간선의 색과 굵기로 표현됩니다. 그림 10을 통해 볼 수 있듯이, grand-nl 모델이 Laplacian diffusion 모델에 비해 더 좋은 결과를 보여줍니다.

5. Conclusion

본 논문은 열확산 방정식을 그래프에서의 메세지 전달 방식으로 확장하여, 연속적인 layer를 구성하는 새로운 GNN을 제안했습니다. 이를 통해 다음과 같은 contribution과 limitation을 가집니다.

Contribution

• 그래프 학습에서 발생했던 여러 가지 문제들(e.g. oversmoothing, bottlenecks, etc.)을 다룰 수 있는 새로운 관점(Neural Diffusion)을 제시

• 새로운 architecture

  • 현존하는 많은 GNN을 discrete Graph 확산 방정식으로 표현 가능

  • 다양한 효율적인 PDE solver를 적용할 수 있는 자유도 (multistep, adaptive, implicit, multigrid, etc.)

  • implicit schemes = multi-hop filters

• 탄탄한 이론적 토대를 가진 물리적 현상 (열 확산)을 바탕으로 새로운 방법론의 이론적 확실성을 제공 (e.g. stability, convergence, etc.)

• GNN 분야에 잘 알려지지 않은 다른 분야와 깊은 연계를 보임(e.g. differential geometry and algebraic topology)

Limitation

• 은닉층의 embedding vector의 크기가 모든 layer에 걸처 동일 (GNN에서 보통의 상황)

• 모든 layer가 같은 parameter set을 가짐 (다만, 이를 통해 10-20배 적은 parameter를 학습)

추가적으로 본 블로그 포스팅을 통해, 본 논문에서 생략된 열확산 방정식이 그래프로 유도되는 과정 및 Graph Diffusion Convolution(GDC)9과의 연관성을 살펴보았습니다.

---

Author Information

• 오윤학(Yunhak Oh)

  • M.S. Student in DSAIL at KAIST

  • Research Topic: Artificial Intelligence, Data Mining, Graph Neural Networks

6. Reference & Additional materials

1: 위키피디아 편미분 방정식

2: https://www.sciencedirect.com/topics/mathematics/diffusion

3: 위키피디아 발산

4: 공돌이의 수학정리노트: 열방정식, 파동방정식의 의미

5: Li, Qimai, Zhichao Han, and Xiao-Ming Wu. "Deeper insights into graph convolutional networks for semi-supervised learning." Thirty-Second AAAI conference on artificial intelligence. 2018.

6: Alon, Uri, and Eran Yahav. "On the bottleneck of graph neural networks and its practical implications." arXiv preprint arXiv:2006.05205 (2020).

7: Matthew Thorpe and Tan Minh Nguyen and Hedi Xia and Thomas Strohmer and Andrea Bertozzi and Stanley Osher and Bao Wang. "GRAND++: Graph Neural Diffusion with A Source Term." International Conference on Learning Representations. 2020.

8: Michael Bronstein | Neural diffusion PDEs, differential geometry, and graph neural networks [Youtube]

9: Klicpera, Johannes, Stefan Weißenberger, and Stephan Günnemann. "Diffusion improves graph learning." arXiv preprint arXiv:1911.05485 (2019).

10: Chung, Fan. "The heat kernel as the pagerank of a graph." Proceedings of the National Academy of Sciences 104.50 (2007): 19735-19740.

11: Graph Neural Networks and Diffusion PDEs | Benjamin Chamberlain & James Rowbottom [Youtube]

12: Chen, Ricky TQ, et al. "Neural ordinary differential equations." Advances in neural information processing systems 31 (2018).

13: Vaswani, Ashish, et al. "Attention is all you need." Advances in neural information processing systems 30 (2017).